في عالم البرمجة والخوارزميات، تُعتبر خوارزمية Dijkstra واحدة من أهم الخوارزميات التي تُستخدم لحساب الطريق الأقصر بين نقطتين في شبكة. سواء كنت مبرمجًا مبتدئًا أو محترفًا، فإن فهم هذه الخوارزمية يمكن أن يكون مفتاحًا لتحسين كفاءة أنظمتك وحل المشكلات المعقدة بفعالية. في هذا المقال، سنقدم شرحًا تفصيليًا عن خوارزمية Dijkstra، كيفية عملها، وأبرز تطبيقاتها في الحياة العملية.
ما هي خوارزمية Dijkstra؟
خوارزمية Dijkstra هي خوارزمية رياضية ابتكرها عالم الحاسوب الهولندي إدسخر ديكسترا عام 1956، وتهدف إلى إيجاد أقصر مسار بين نقطتين في رسم بياني (Graph) موجه أو غير موجه، بشرط أن تكون الأوزان على الحواف (Edges) غير سالبة.
استخداماتها الأساسية
- إيجاد الطريق الأقصر بين نقطتين في شبكات النقل.
- تحسين أداء الشبكات الإلكترونية عبر اختيار أفضل مسارات البيانات.
- تطبيقات الخرائط (مثل Google Maps) لحساب المسارات الأقصر.
كيف تعمل خوارزمية Dijkstra؟
1. التمثيل البياني
- تعتمد الخوارزمية على تمثيل الشبكة باستخدام الرسم البياني (Graph).
- العقد (Nodes): تمثل النقاط أو المواقع.
- الحواف (Edges): تمثل الطرق أو المسارات بين النقاط.
2. خطوات التنفيذ
التهيئة (Initialization):
- قم بتعيين تكلفة (Cost) البداية لكل عقدة إلى “ما لا نهاية” (Infinity) باستثناء العقدة الأولى، التي تكون تكلفتها صفرًا.
- استخدم قائمة لتتبع العقد التي تم زيارتها.
البحث (Iteration):
- اختر العقدة ذات التكلفة الأقل والتي لم تُزر بعد.
- قم بحساب تكلفة الوصول إلى العقد المجاورة وتحديث تكلفتها إذا كان الطريق الجديد أقصر.
التكرار حتى النهاية:
- استمر في العملية حتى يتم زيارة جميع العقد.
3. الإخراج (Output):
- عند اكتمال العملية، ستكون لديك أقصر تكلفة ومسار لكل عقدة انطلاقًا من العقدة الأولية.
مثال عملي على خوارزمية Dijkstra
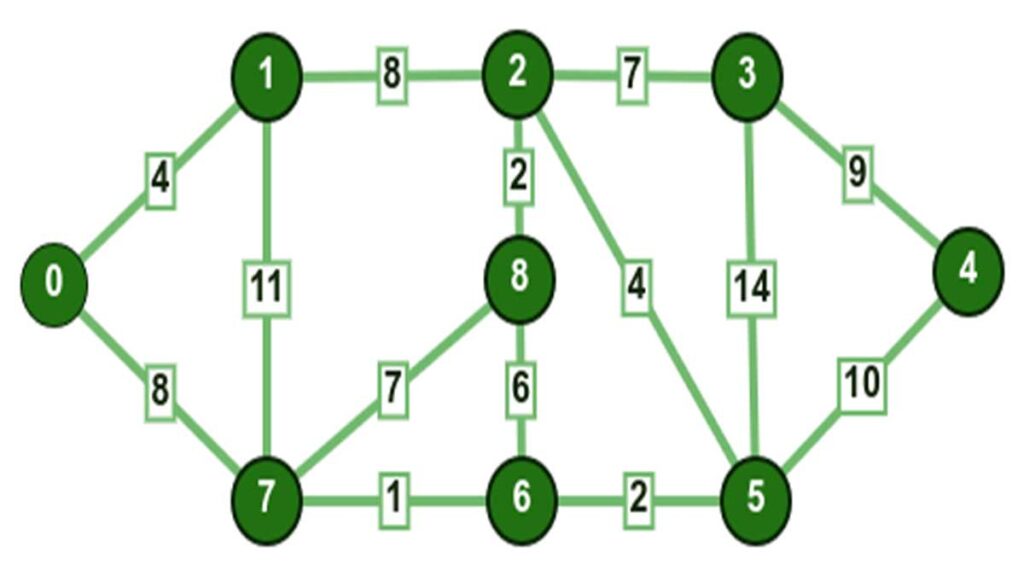
لنفترض أن لدينا الرسم البياني التالي:
| الطريق | التكلفة |
|---|---|
| A → B | 4 |
| A → C | 2 |
| B → C | 5 |
| B → D | 10 |
| C → D | 3 |
خطوات الحل:
- البدء من A، التكلفة = 0.
- تحديث تكلفة B وC:
- B = 4، C = 2.
- الانتقال إلى C (الأقل تكلفة).
- تحديث تكلفة D عبر C: D = 2 + 3 = 5.
- الانتقال إلى B ثم إلى D.
- الإخراج: الطريق الأقصر من A إلى D هو A → C → D، والتكلفة الإجمالية = 5.
مميزات وعيوب خوارزمية Dijkstra
المميزات
- كفاءة عالية: مناسبة للشبكات ذات عدد محدود من العقد.
- مرونة: يمكن تطبيقها على العديد من التطبيقات الواقعية.
العيوب
- قيود الأوزان السالبة: لا تعمل مع الرسوم البيانية التي تحتوي على أوزان سالبة.
- تعقيد حسابي: يصبح الأداء أقل كفاءة في الرسوم البيانية الكبيرة جدًا.
تطبيقات خوارزمية Dijkstra
- أنظمة الملاحة:
- مثل Google Maps لإيجاد الطريق الأسرع.
- الشبكات الإلكترونية:
- تحسين توجيه البيانات في الإنترنت.
- ألعاب الفيديو:
- تحديد المسارات المثلى لحركة الشخصيات أو الموارد.
- التخطيط اللوجستي:
- تحسين عمليات الشحن والنقل.
أسئلة وأجوبة حول خوارزمية Dijkstra
1. هل يمكن استخدام خوارزمية Dijkstra مع الأوزان السالبة؟
- لا، خوارزمية ديكسترا تعمل فقط مع الرسوم البيانية ذات الأوزان غير السالبة. يمكن استخدام خوارزميات أخرى مثل Bellman-Ford للأوزان السالبة.
2. ما هي المعقدية الزمنية لخوارزمية Dijkstra؟
- تعتمد على بنية البيانات المستخدمة:
- باستخدام قائمة أولوية بسيطة: O(V2)O(V^2).
- باستخدام قائمة أولوية مع كومة (Heap): O((V+E)logV)O((V + E) \log V)، حيث VV هو عدد العقد وEE عدد الحواف.
3. هل تعمل خوارزمية Dijkstra مع الرسوم البيانية غير الموجهة؟
- نعم، طالما أن الأوزان غير سالبة، يمكن استخدامها مع الرسوم البيانية غير الموجهة.
4. هل يمكن استخدام الخوارزمية في الشبكات الديناميكية؟
- يمكن ذلك، لكن يتطلب إعادة تشغيل الخوارزمية عند كل تغيير في الشبكة.
5. ما هي البدائل لخوارزمية Dijkstra؟
- من البدائل:
- A* (للرسوم البيانية الكبيرة مع استخدام الدالة الإرشادية).
- Bellman-Ford (للأوزان السالبة).
6. ما الفارق بين Dijkstra وخوارزمية Floyd-Warshall؟
- Dijkstra تُستخدم لحساب المسار الأقصر من نقطة واحدة، بينما Floyd-Warshall تُستخدم لحساب جميع المسارات الأقصر بين جميع النقاط.
7. هل تُستخدم خوارزمية Dijkstra في الذكاء الاصطناعي؟
- نعم، تُستخدم في الذكاء الاصطناعي، خاصة في تخطيط المسارات في الروبوتات أو ألعاب الفيديو.
8. ما الأدوات أو المكتبات البرمجية التي تدعم تنفيذ Dijkstra؟
- Python: مكتبة NetworkX.
- Java: مكتبة JGraphT.
9. كيف يمكن تحسين أداء الخوارزمية؟
- استخدام هياكل بيانات مثل Fibonacci Heap لتقليل التعقيد الزمني.
10. هل يمكن استخدام Dijkstra في التطبيقات الحقيقية؟
- نعم، تُستخدم بشكل واسع في الملاحة، الشبكات، وحتى في تحليل الأنظمة الاجتماعية.
خاتمة
خوارزمية Dijkstra ليست مجرد أداة نظرية، بل هي أحد الحلول العملية التي تُستخدم على نطاق واسع لحل مشاكل المسار الأقصر في العديد من المجالات. إذا كنت مبرمجًا طموحًا، فإن تعلم هذه الخوارزمية سيفتح لك آفاقًا جديدة في تصميم الحلول الذكية والكفؤة.
هل لديك تطبيق ترغب في تحسينه باستخدام Dijkstra؟ شاركنا أفكارك في التعليقات!
مواضيع ذات صلة:
ما هو الذكاء الإصطناعي وكيف يعمل؟
طريقة إيقاف تحديثات ويندوز 11 نهائياً أو مؤقتاً